How To Solve Installment Problems

Brand Style For The Matrix — A Complete Guide to Solving 2D Assortment Coding Problems

Photo by Josh Riemer on Unsplash

Most matrix problems can be intimidating at first glance. Withal, they are not that hard to solve at all! In this article, I volition break downwardly the steps to solve these problems starting with an overview of the matrix and how it is used.

First things showtime! Let'south go an overview of what a matrix is all about.

What is a matrix?

Definition from Wikipedia: "In mathematics, a matrix (plural matrices) is a rectangular array of numbers, symbols, or expressions, bundled in rows and columns."

In most places, the terms matrix and ii-D arrays are used interchangeably. A ii-dimensional array tin office exactly similar a matrix. Two-dimensional arrays can be visualized equally a tabular array consisting of rows and columns.

Examples of matrices

Where do we run into matrices in real life

• Predominantly in database systems where data in tables are stored at intersections of a particular row and cavalcade.
• In graphics where matrices represent pixels.
• In a movie ticketing system (row-seat-number) or whatsoever booking system(autobus/train/airlines) that uses row and column for seat identification.

Initialization and Traversal

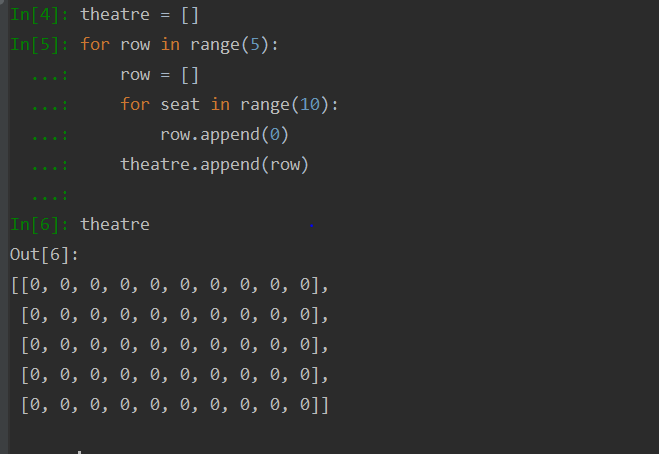
2D arrays are represented every bit a listing of lists. Each list typically represents a row and each element of the listing is a column. In this example, we will prepare a theatre seating of 5 rows with 10 seats in each row.

Initialize 2nd array

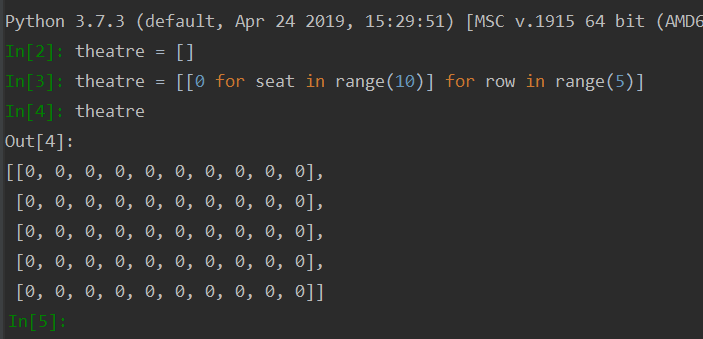
The in a higher place can also be accomplished with a nested listing comprehension:

Initialize a 2D array with listing comprehension

Suppose, now we need to update that the last 2 rows are booked by setting a value of one. This is how to do information technology:

Update 2D Array

Warm-up problem

Now that nosotros have covered the nuts, permit's outset with an piece of cake trouble.

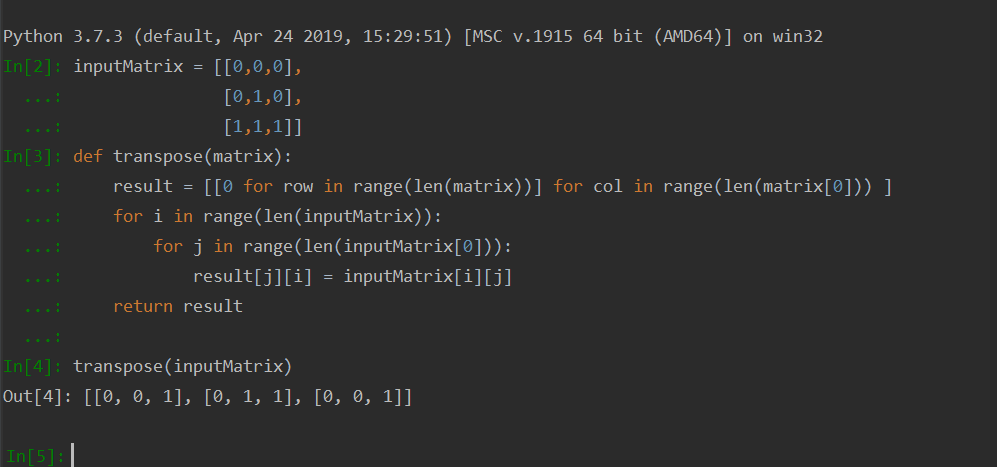
Transpose a matrix

Transposing a matrix is to swap its row values with its column values.

          For every cell result[i][j] we need to replace the value with  input[j][i]            
where input is the matrix to be transposed and            
result is the placeholder for the transposed matrix        

Here's the walkthrough:

Matrix Transpose

Here's the lawmaking:

matrixTranspose.py

Moving on — to searching and updating matrices.

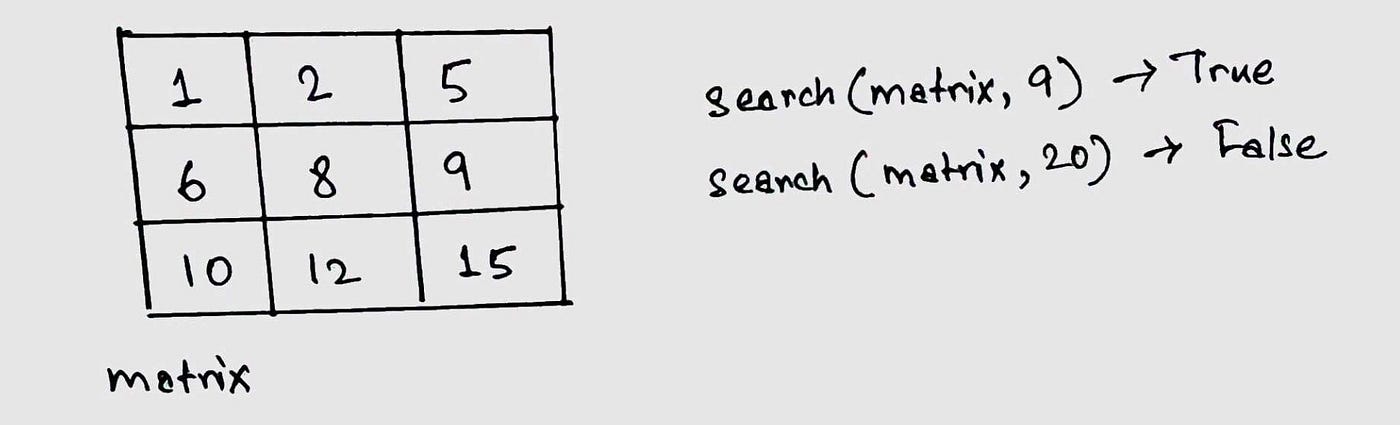
74. Search a second Matrix

In this problem, we need to search for a value in a sorted matrix. A sorted matrix substantially means that the value at cell A[i][j] will always be greater than the values of all cells preceding it.

Input and expected output

Solution1: The animate being-forcefulness arroyo to solving this is to iterate through each row and each column until we take found the target element or reached the end of the matrix.

search Matrix — Animal Force

However, this is O(M*N) and does non employ any of the structural information of the matrix provided in the problem description.

How can we exercise this better? In the matrix, every element in a row is sorted and all the rows are sorted in ascending lodge. What practise we use to search a value in sorted arrays? Enter Binary Search!

Solution2: Initialize start to 0 and end to Thousand-one where Thousand= number of rows. Find the centre row and then apply a binary search to search for the target element in the row. If the target element is found, return True else modify the middle row as needed and continue the search till get-go ≤ cease. And so, the outer binary search searches for the row while the inner binary search searches for the element within a row. Here'south the walkthrough:

binary search solution walkthrough

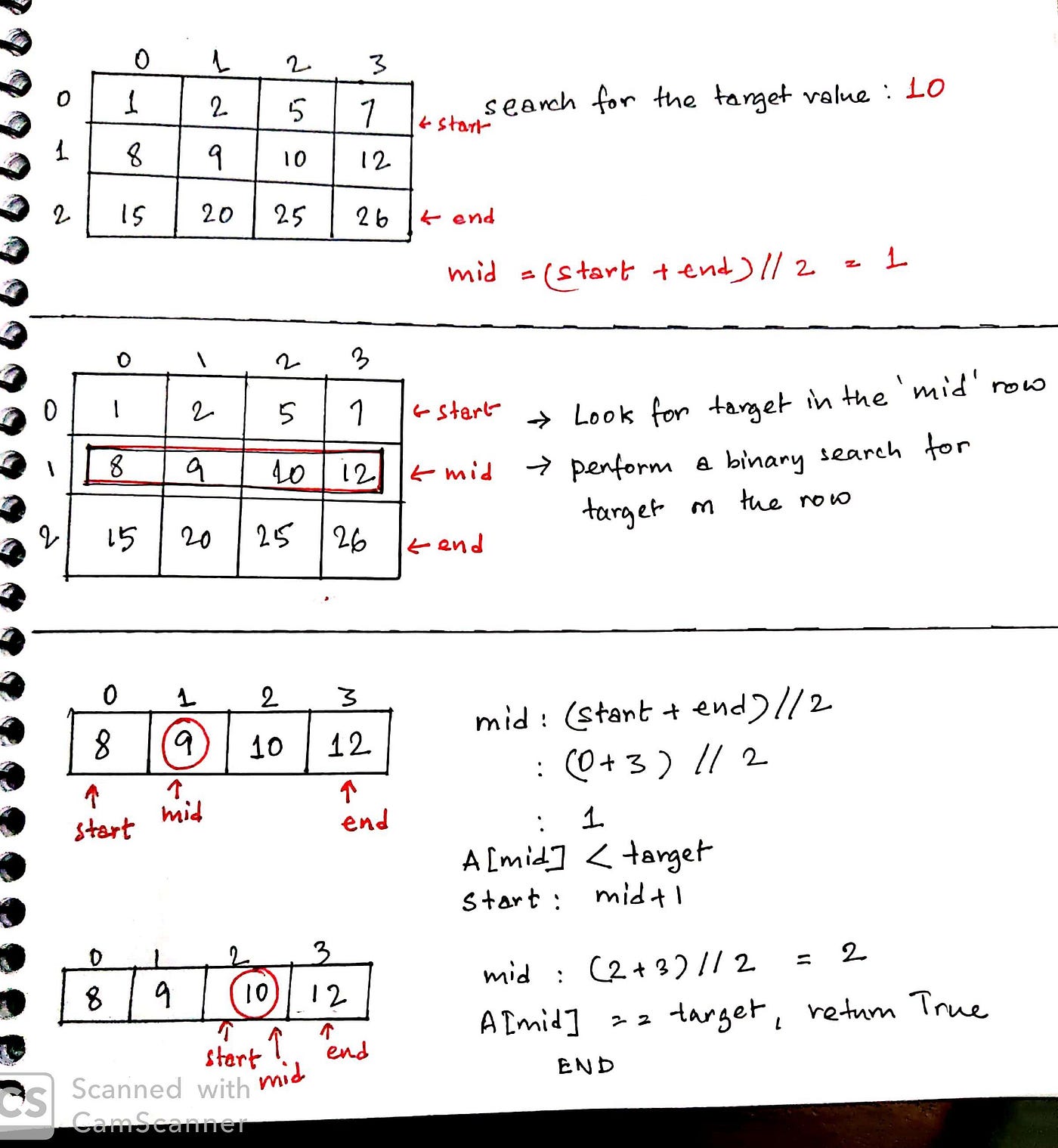
And here's the code:

search Matrix — Binary search

Solution3: If we expect closely at the matrix, there is an easier solution bachelor. Notice that the elements go smaller as nosotros move left in a row and larger as we move down a cavalcade. Utilizing this info we can traverse the matrix, changing direction depending on the value at a cell. Hither's the walkthrough:

search Matrix — use direction

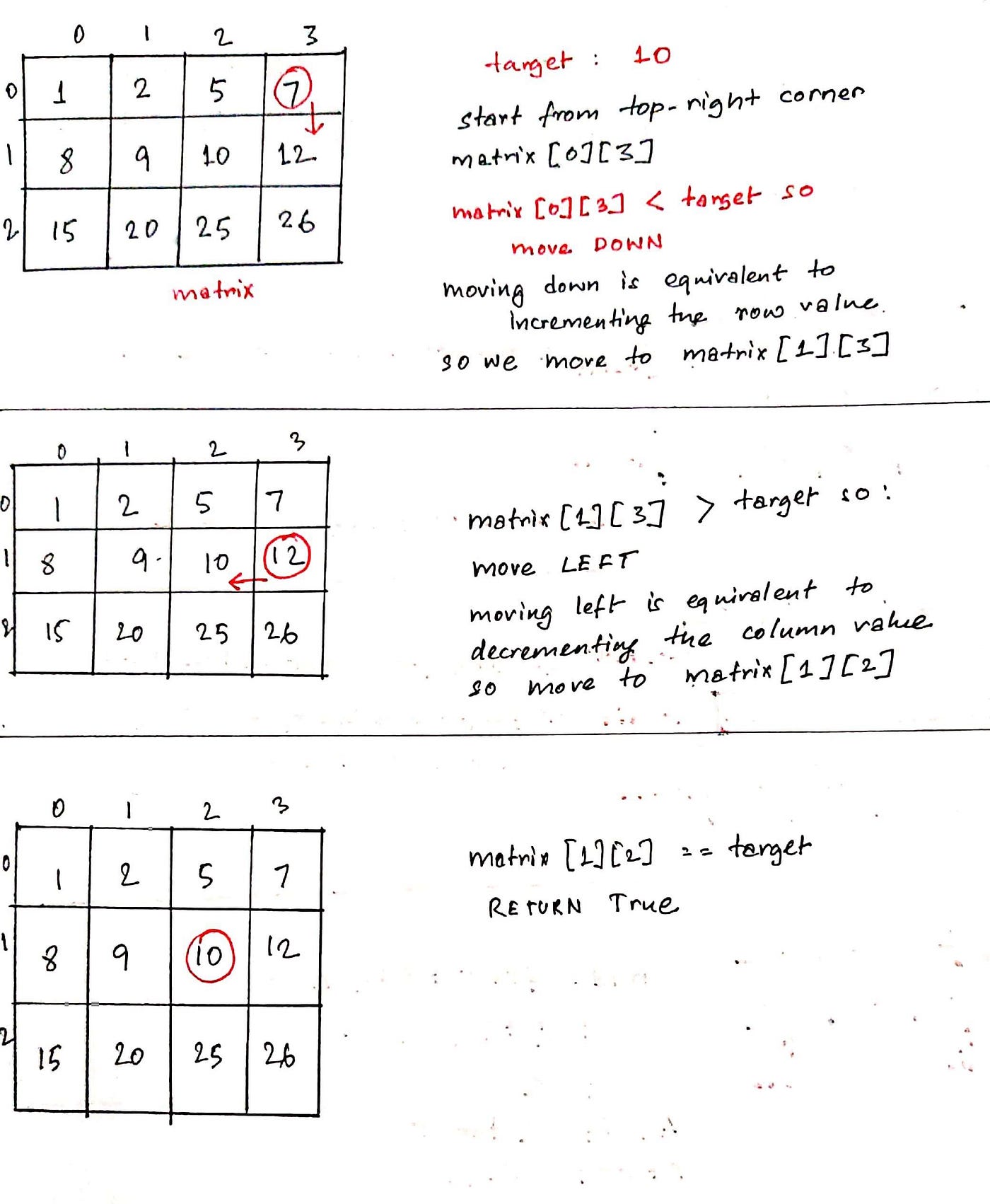
Here's the code:

search Matrix using direction

Note: We do not start from the top left of the matrix merely instead from the meridian correct. Why? Considering, if nosotros traverse from the acme left, we can move to the correct or motility downwardly and in both cases, values volition only increment.

240. Search a 2D Matrix II

This is pretty like to the previous problem. Unlike the previous problem where all the elements were sorted, here a preceding row tin can have higher values than the rows following information technology. Then nosotros cannot use a binary search to decide a detail row for searching the target.

Let'south focus on the direction of the growth of the elements. The values increase downwards and values decrease as nosotros move left. Using this info we can employ the same algorithm as the higher up problem to solve this. Here's the walkthrough:

search matrix II walkthrough

Here's the code:

searchMatrixII

73. Prepare Matrix Zeroes

My initial attempt to solve this problem was to traverse the array and if a 0 is found and then update the unabridged row to 0. Bad idea! This volition lose the information of which columns had a 0 value. Then, earlier we actually update the array, we need something to maintain a record of which rows and columns contain 0.

Here's the walkthrough:

setZeroMatrix walkthrough

Here'due south the code:

setZeros.py

At present let's look at traversing a matrix in dissimilar ways: spirally and diagonally.

54. Spiral Matrix

Problem input and expected output

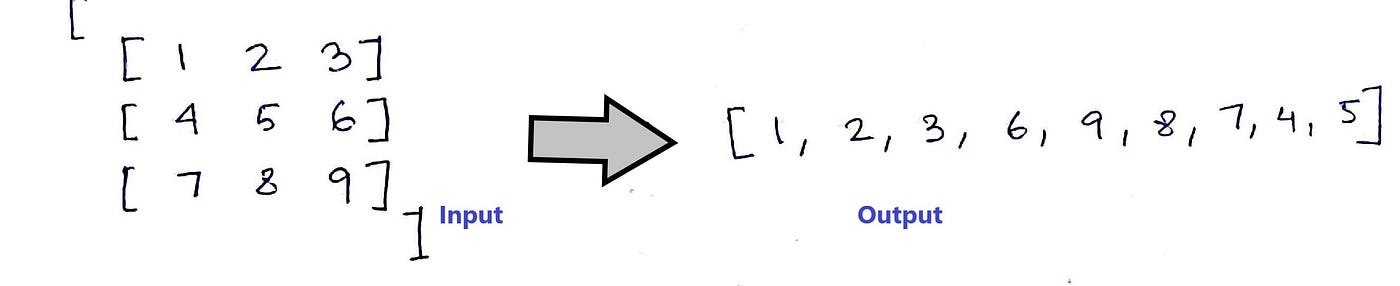
Note: There can exist several ways to solve this trouble. However, what I am sharing here seems the near intuitive solution. So let's look at it stride by step.

Step1: Imagine nosotros were solving this by hand in which instance we can only move in iv directions: nosotros outset with right, and then move downward, then left and finally upward(followed by right again).

where can we movement?

Step2: How long practice we go along doing this? Expect at the image below.

when do we stop traversing

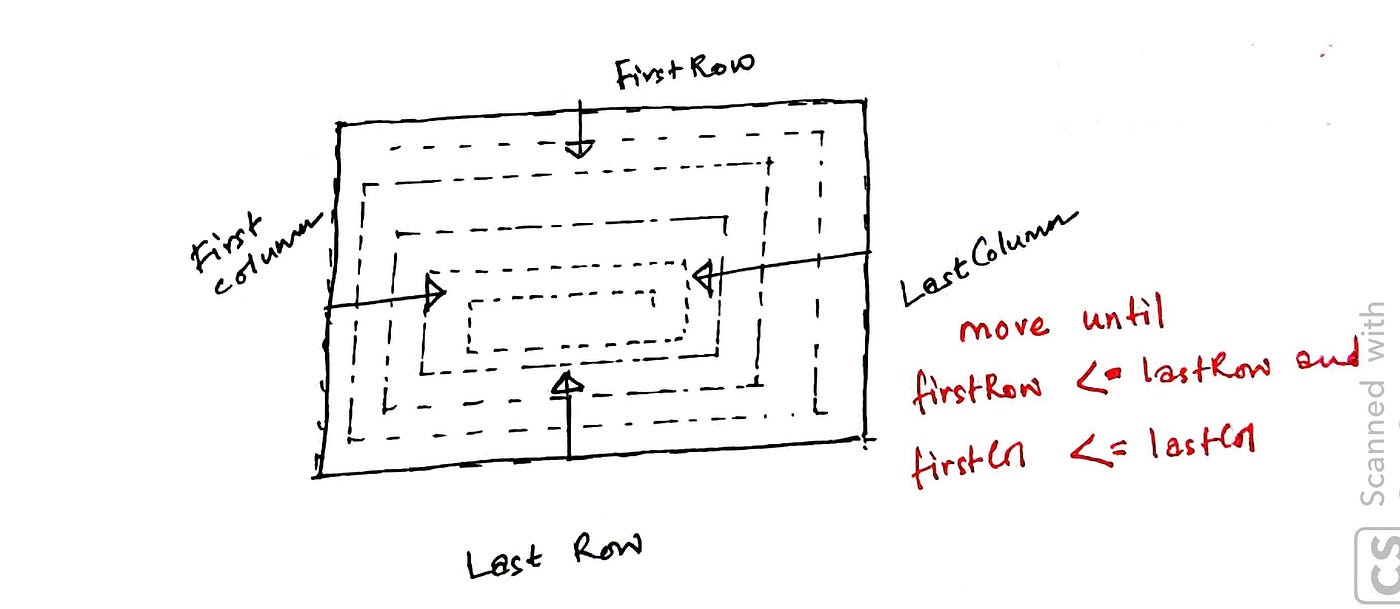
Consider the matrix to be the shrinking infinite between the boundaries that are moving in. We know that we have traversed the entire matrix when these boundaries encounter.

Step3: Now we already discussed the directions to move in. Permit's look at how the boundaries modify when we traverse in direction.

boundary changes when moving spirally

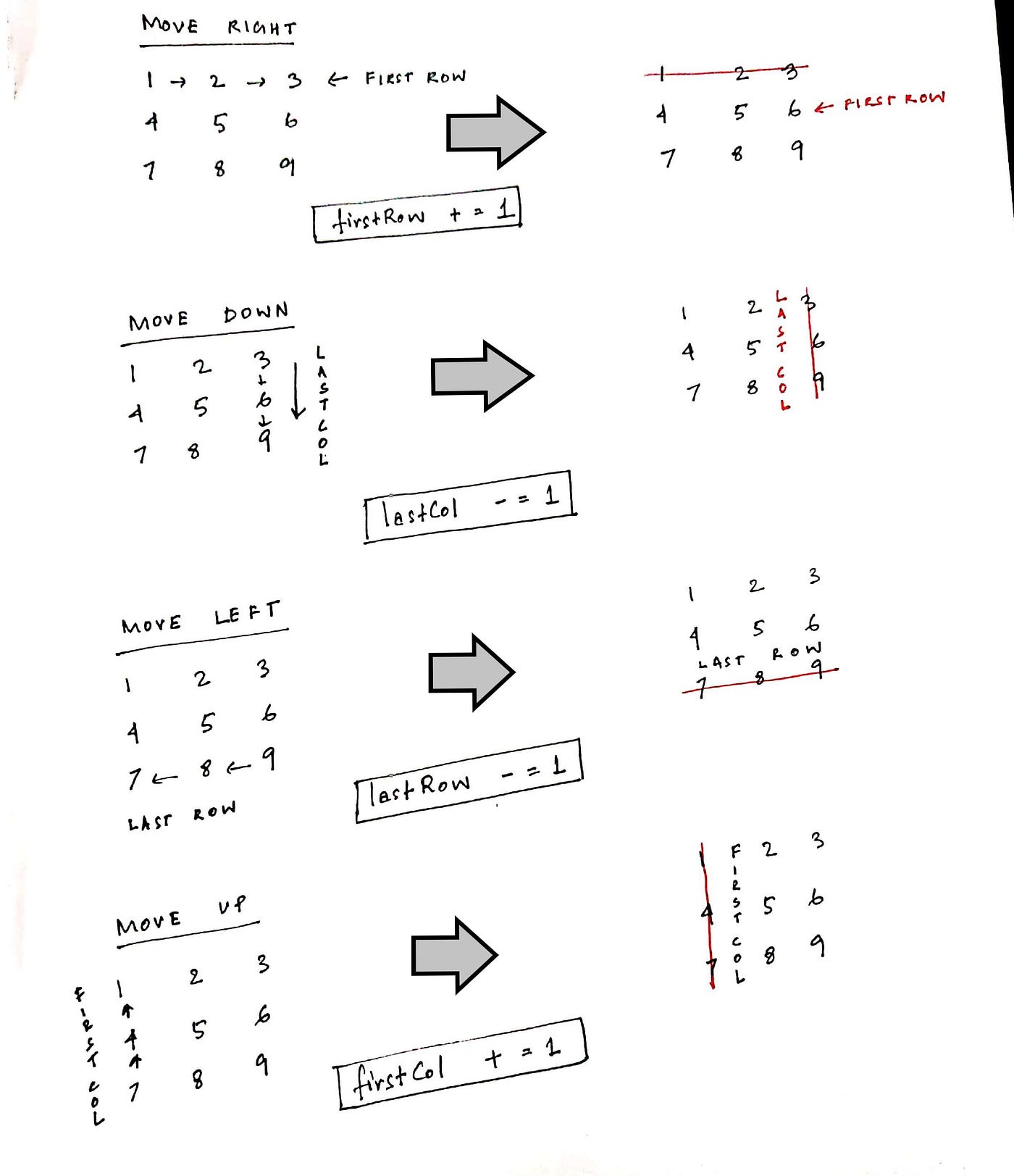
Step4: Finally, how do we avert traversing an element that we accept already passed through before? To do this we maintain another matrix where we store the information of which positions are already traversed with a boolean value.

Here's the lawmaking

spiralMatrix1

59. Spiral Matrix II

This problem is pretty similar to the commencement. Instead of traversing the matrix, here we demand to build a square of 'n' matrix. To do this we first build a matrix of north*n boolean values to shop our result matrix and keep filling information technology as we movement spirally — correct →down →left →up →right….until we have filled values up to n*n.

Here's the walkthrough:

Generate matrix walkthrough

Here'southward the lawmaking:

spiralMatrix2

498. Diagonal Traverse

Input and expected output

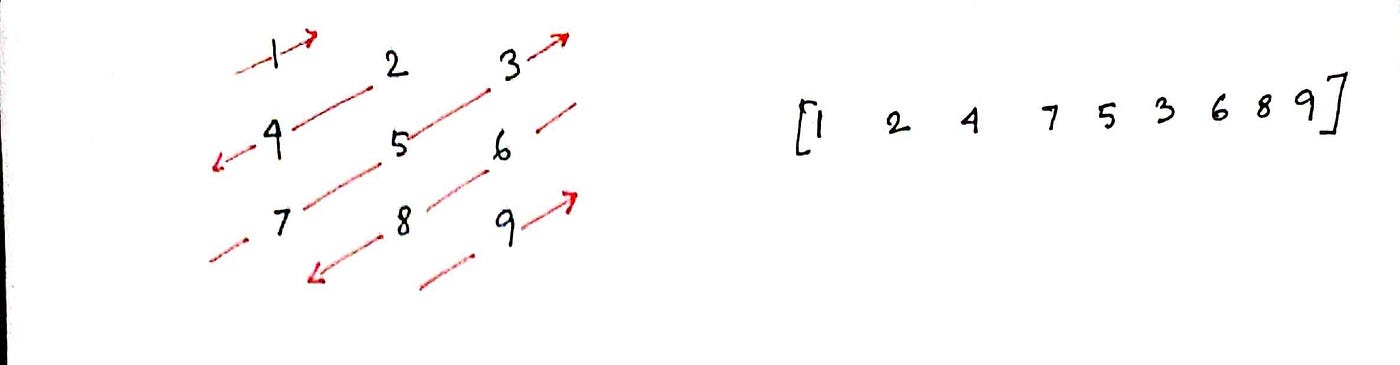
Solution1: Solving this by hand we can meet that we tin can move in 4 directions: Diagonally Up(DU), Diagonally Downward(DD), Correct(R) by ane step, Downwards(D) past 1 step.

Now let's see how the row and column ids alter equally we motility in these directions:

diagonal matrix walkthrough

Here is the lawmaking:

diagonalMatrix1

Solution2: An easier solution exists which depends on the fact that the sum of the coordinates of every element in a diagonal will exist the same.

Here is the implementation:

diagonalMatrix.py

Cheers for the read and I promise this helped. Concluding with this quote from The Matrix, retrieve this when solving matrix problems or any problem :).

Neo: What is the Matrix?
Trinity: The answer is out there, Neo. It's looking for you, and information technology will detect you if you lot want it to.

Resources

1. https://www.ict.social/python/basics/multidimensional-lists-in-python
2. https://www.hackerearth.com/practice/data-structures/arrays/multi-dimensional/tutorial/
3. https://www.hackerearth.com/practise/data-structures/arrays/multi-dimensional/tutorial/
4. https://en.wikipedia.org/wiki/Matrix_(mathematics)
5. https://leetcode.com/

Source: https://levelup.gitconnected.com/make-way-for-the-matrix-a-complete-guide-to-solving-2d-array-coding-problems-725096d122d9

Posted by: hamilscolon.blogspot.com

Share this post